Probability Definition
There are 3 definitions of probability:
Classical Probability
Empirical Probability
Subjective Probability
Classical Probability
Probability is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes.
Example
Probability of head in a coin toss
- Possible outcome = {H, T}
- Favourable outcome = {H}
- Probability of head = 1/2
Empirical Probability
Probability is defined as the ratio of the number of times favorable outcomes occurred to the total number of times experimentation performed.
Example
We toss a coin 3 times and get the following results

- Probability of head = 2/3
- Probability of tail = 1/3
Subjective Probability
Probability is defined based on an individual’s own experience or personal judgment.
Example:
Probability of reader understanding the definition of probability = 0.85
Axioms of probability
Let,
- S be the sample space
- A and B are events that belong to sample space

There are 3 axioms of probability:
- 0 ≤ P(A) ≤ 1, 0 ≤ P(B) ≤ 1
- P(S) = 1
- P(A U B) = P(A) + P(B) - P(AB)
Problem
John is planning to visit his grandparent on either 30th May or 31st May. John beliefs that there is a chance of
- Rain on 30th May is 30 %
- Rain on 31st May is 40 %
- Rain on both 30th May and 31st May is 20 %
- Rain on either 30th May or 31st May is 60 %
Question: What is wrong with his beliefs?
Solution
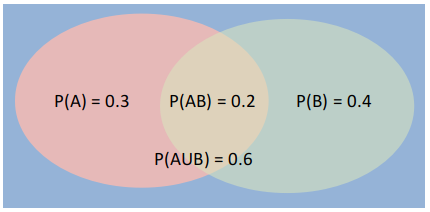
A = Rain on 30th May
B = Rain on 31st May
P(A) = 0.3
P(B) = 0.4
P(AB) = 0.2
P(A U B) = 0.6
But,
P(A U B) = P(A) + P(B) - P(AB)
P(A U B) = 0.3 + 0.4 - 0.2
P(A U B) = 0.5 which is not equal to 0.6
Question: How John needs to modify his belife to be in consistent with axioms of probability?
Solution
P(A) = 0.3
P(B) = 0.4
P(AB) = 0.1
P(A U B) = 0.6

But,
P(A U B) = P(A) + P(B) - P(AB)
P(A U B) = 0.3 + 0.4 - 0.1
P(A U B) = 0.6
